[웹 프로그래밍 스쿨 19주차] 파이썬으로 BST(Binary Search Tree) insert, delete, search 기능 구현 해보기!
웹 프로그래밍 스쿨 19주 차 포스팅입니다!😃
이번 주 자료구조 시간에는 자료구조의 노드들을 재방문 없이 방문하는 순회와 관련된 알고리즘과
List와 Linked list의 장단점, BST와의 비교, Heap에 대해 공부했는데요!
그중 Database와 File system에서 사용되는 자료구조인 b+ tree의 기초가 되는 BST에 대해
정리해봤습니다.
1. BST (Binary Search Tree)의 조건
-
모든 원소는 서로 다른 키를 가진다.
-
왼쪽 서브 트리에 있는 모든 키들은 루트의 키보다 작다.
-
오른쪽 서브 트리에 있는 모든 키들은 루트의 키보다 크다.
-
왼쪽 서브 트리와 오른쪽 서브 트리도 이진 탐색 트리이다.
2. BST의 장점
BST는 파이썬의 list와 linked list 둘의 단점을 모두 보완할 수 있습니다.
list는 오프셋을 통한 인덱싱 기능으로 list 안을 search 할 때 O(1)의 시간 복잡도를 갖지만
insert나 delete 할 때 맨 뒤에 값을 더하거나 빼는 상황이 아니라면
최악의 경우 list 내의 모든 요소를 한 칸씩 이동시켜야 하는 상황이 생겨 O(n)의 시간 복잡도를 갖는
단점이 있습니다.
linked list는 반대로 insert와 delete 할 때 해당 노드와 앞 뒤 노드를 연결시키거나
끊는 방법으로 빠르게 처리 가능하지만 search 할 때 최악의 경우 header부터 끝까지 이동해야
할 수 있으므로 O(n)의 시간복잡도를 갖게 됩니다.
search나 insert/delete 한쪽만을 사용해서 기능을 구현하는 경우는 적은데,
BST search와 insert, delete 기능의 빅 O가 모두 O(logN)이라는 점에서 이점이 있습니다.
3. 파이썬으로 BST 기능 구현
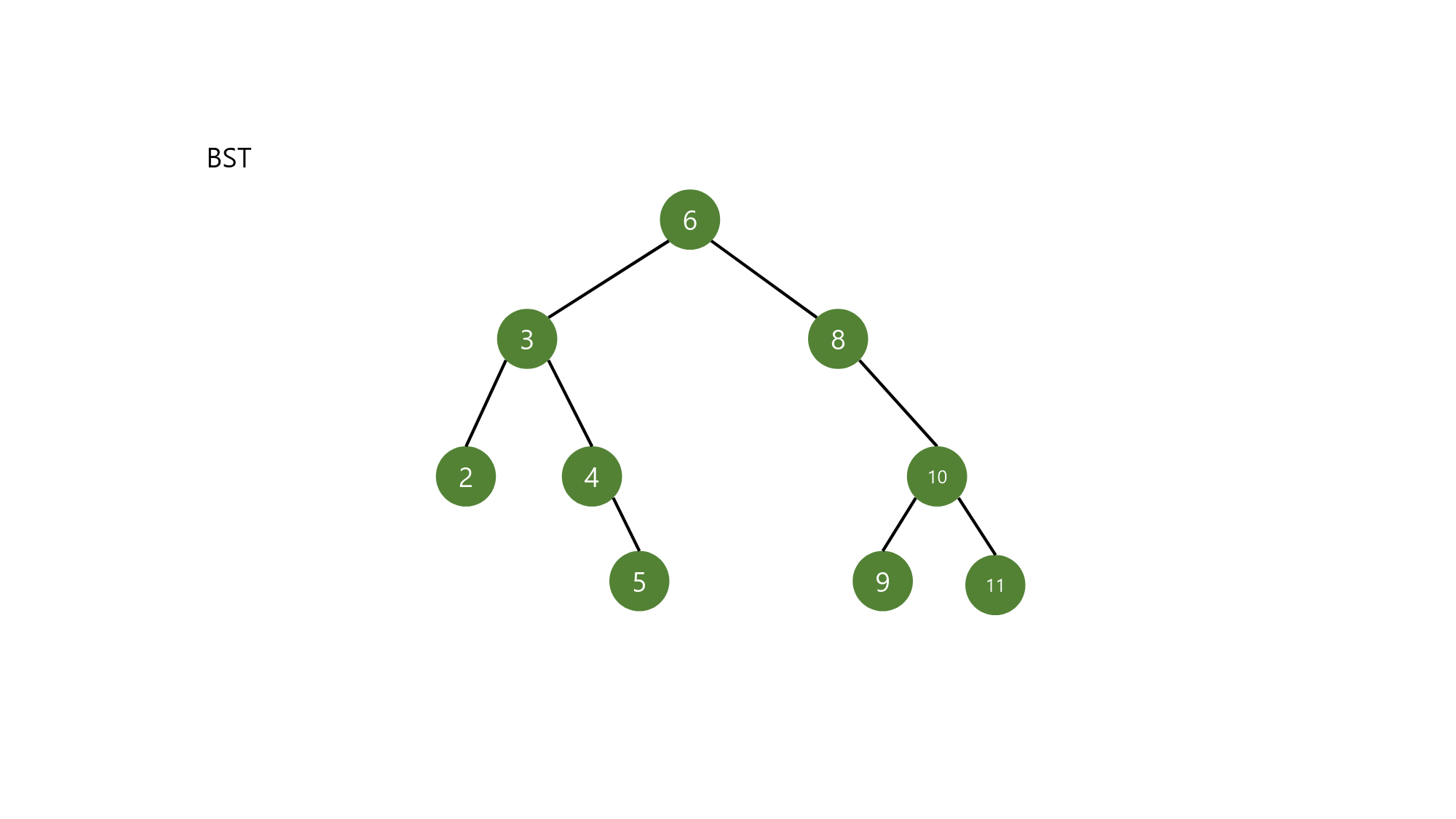
class BST:
def __init__(self):
self.__root = None
@property
def root(self):
return self.__root
def insert(self, key):
new_node = TreeNode(key) # 1
cur = self.__root # 2
par = self.__root # 3
if not self.__root :
self.__root = new_node
return
while cur : # 4
if cur.key > key: # 5
par = cur
cur = cur.left
else :
par = cur
cur = cur.right
if par.key < key: # 6
par.right = new_node
else :
par.left = new_node
#1. 삽입할 번호를 key로 가지는 노드를 생성합니다.
#2. 루트부터 검색을 시작하기 위해 cur에 root노드를 할당합니다.
#3. 삽입할 위치를 찾았을 때 노드를 할당하기 위해 par을 설정합니다.
#4. cur이 None값을 가지는 위치에 도착할 때까지 반복합니다.
#5. cur위치의 key 값이 삽입할 노드의 key값 보다 크다면 cur을 왼쪽으로, 작다면 cur을 오른쪽으로 이동시키고
par을 cur이 있던 위치에 이동시킵니다.
#6. while문이 멈췄다면 cur은 None이 되었으므로 cur의 이전 위치인 par의 key와 삽입할 노드의 key값을 비교해서
par의 값이 크다면 왼쪽에, 작다면 오른쪽에 new_node를 할당합니다.
def search(self, target):
cur = self.__root
while cur :
if cur.key == target :
return cur
elif cur.key > target :
cur = cur.left
else :
cur = cur.right
return None
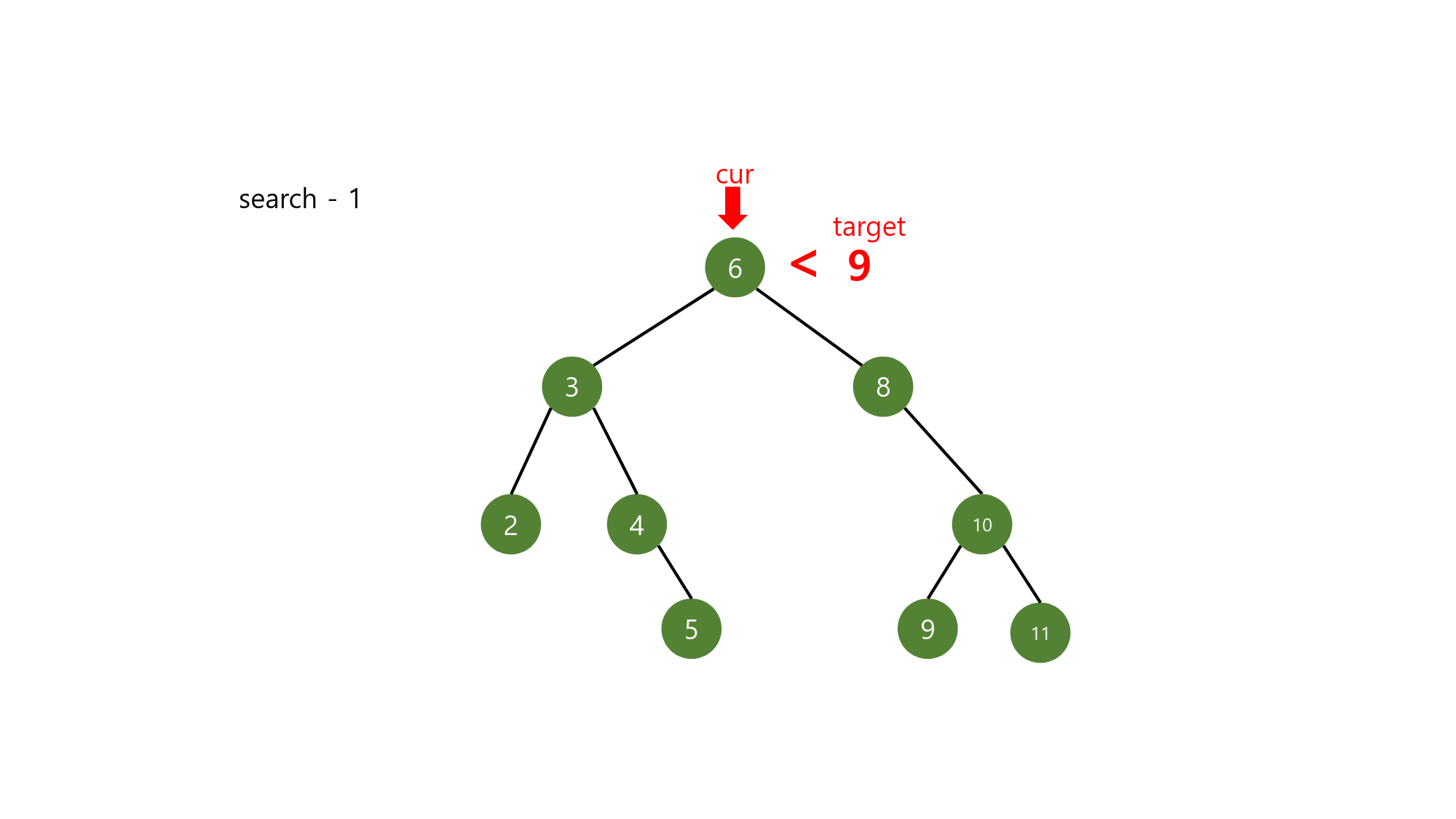
search 기능도 간단합니다.
그림처럼 BST에서 9라는 값을 찾고 싶을 때
1. 루트 노드를 먼저 9와 비교하고
2. 찾으려는 값이 루트 노드보다 더 크므로 cur을 오른쪽으로 이동합니다.
3. 다시 현재 cur의 key값인 8과 비교하고 cur을 오른쪽으로 이동시킨 후에 10과 비교합니다
4. 이번엔 찾으려는 값이 cur의 key값인 10보다 작으므로 cur을 왼쪽으로 이동시킨 후에
5. cur값을 비교했더니 찾으려는 값과 일치하므로 해당 노드를 반환합니다.
def __delete_recursion(self, cur, target):
# base case
if not cur:
return None
elif target < cur.key:
cur.left = self.__delete_recursion(cur.left, target)
elif target > cur.key:
cur.right = self.__delete_recursion(cur.right, target)
else :
# 1. 삭제노드가 리프노드인 경우
if not cur.left and not cur.right:
cur = None
# 2. 삭제노드의 자식이 하나 일 때
# 오른쪽 자식이 있는 경우
elif not cur.left:
cur = cur.right
elif not cur.right :
cur = cur.left
else:
# 대체 노드를 찾는다
rep = cur.left
while rep.right:
rep=rep.right
# 삭제 노드와 대체 노드의 키를 교환
cur.key, rep.key = rep.key, cur.key
cur.left = self.__delete_recursion(cur.left, rep.key)
return cur
삭제는 3가지 경우가 있습니다.
우선 cur와 key값을 비교해서 cur보다 값이 작으면 왼쪽으로 크면 오른쪽으로 반복적으로 이동해서 삭제할 노드를 찾습니다.
1. 자식 노드가 하나도 없을 때
-
삭제할 노드가 자식 노드를 가지고 있지 않다면 부모 노드와의 링크를 끊어주는 것만으로 노드를 삭제할 수 있습니다.
(파이썬에서는 가비지 컬렉터가 레퍼런스 카운터가 0이 된 노드를 자동으로 삭제시켜줍니다.)
2. 자식 노드가 하나만 있을 때
-
부모 노드와의 링크를 끊고 부모 노드의 링크를 자식 노드에 연결시켜 줍니다.

3. 양쪽에 다 있을 때
-
삭제시킬 노드의 빈자리를 채울 노드가 필요합니다.
-
삭제시킬 노드의 왼쪽 서브 트리에서 가장 큰 값이 대체할 수 있습니다.
(왼쪽 자식 노드의 오른쪽 노드를 쭉 타고 내려가다가, null 값을 가지는 오른쪽 자식 노드를 가지는 노드로 대체)
-
삭제시킬 노드의 오른쪽 서브 트리에서 가장 작은 값이 대체할 수 도 있습니다.
(오른쪽 자식 노드의 왼쪽 노드를 쭉 타고 내려가다가, null 값을 가지는 왼쪽 자식을 가지는 노드로 대체)
'패스트 캠퍼스' 카테고리의 다른 글
| [웹 프로그래밍 스쿨 21주차] 팀 프로젝트 중간점검! (0) | 2019.07.28 |
|---|---|
| [웹 프로그래밍 스쿨 20주차] 파이썬으로 우선순위 큐를 위한 heap 구현하기! (1) | 2019.07.21 |
| [웹 프로그래밍 스쿨 18주차] 팀 프로젝트 시작! (0) | 2019.07.07 |
| [웹 프로그래밍 스쿨 17주차] 컴퓨터 시스템 구조(computer system structure)에 대해 알아보기! (0) | 2019.06.30 |
| [웹 프로그래밍 스쿨 16주차] 운영체제(O/S)에 대해 알아보기! (0) | 2019.06.23 |













